Bas me zanima koliko ljudi ce se upecati na ovo?
Mislim da je svima jasno sto vlasnik ove stranice zeli psotici, taj na ruletu nije dobio niti lipe, a vjerujem niti izgubio jer on znade bolje nacine zarade, a to je trazenje naivaca koji ce korisitti ovu metodu koju je opisao na webstranici.
Sta mislite da ovakvi sitevi prolaze? Osobno znam par ljudi koji bi se upecali na ovom.
A ja sam naletio na stranicu preko pop upa kada sam surfao torentima.
Moj pokojni deda uvijek je govorio: ‘Budala i krivi’ drva nikad nece nestati"
Ima brdo takvih sajtova, sto na engleskom sto na nasem, ocito prolazi kad ih je toliko.
A suština je da metoda funkcionira, ako vam kazino dozvoli da igrate na tu metodu
Pretpostavljam da je onaj fazon: igraš uvek na istu boju da povećanjem uloga za duplo svaki put kad izgubiš.
Metoda ne funkcionira, niti statisticki.
A ja sam mislio na upecavanje sto radi vlasnik stranice, a ne ova njegova metoda koja se u biti zove Martingale.
Ili kako je ja zovem ubojica zivota.
Kladionicu ne igram ni dok cedevitu pijem. Nema tu sreće. Više volim stalno gledati AdSense nego ponudu dana…
Tako je …ne radi niti statistički. …a uz martingale, često se zove i bankrot metoda.
Da u “kratko” pojasnim u čemu je caka…i zašto ljudima djeluje da radi.
Prvo…mora se zamisliti neka ograničena banka za sistem, jer unlimited banka ne postoji.
Drugo, zamislit ćemo da zelena (0) ne postoji, tada matematički koeficijenti padaju u ravnopravnost. Tek tada je zaista koeficijent 2 na crveno/crno i koeficijent 36 na broj. Nula to ne odmiče daleko od tih koeficijenata…ali nula je jedina koja okreće statistiku na stranu kuće. (Ukoliko kuća ne vara na druge načine)
Treba imati na umu da kombinacijom brojeva mi možemo zapravo birati koeficijent na koji se kladimo. Ako zatvorimo jedan broj, onda je k=36, ako zatvorimo dva broja k=18 …ako igramo na trećinu k=3 itd.
Ako npr. zatvorimo 35 brojeva od 36, onda smo odigrali prilično siguran koeficijent koji je 1.028 (približno 1.03)
Ajmo sad zamisliti da nam je banka 100 000kn.
Opcija A)
Dolazimo u kasino i stavljamo sve na “crno” …kući idemo praznih đepova, ili sa 200 000kn. Kako god bilo…odigrali smo pošteni koeficijent 2.
Opcija B) Odigramo nešto sigurniju varijantu i uložimo ravnopravno sve na 35 brojeva …ukoliko nas ne zezne onaj 36-ti broj, dobitak je 100 000 x 1.03= 103 000. Vrlo laganih 3 000kn u džepu, ali bome i fini rizik za tih 3000kn.
Koja opklada je bila sigurnija A ili B?
A?
Statistički ako bi odigrali dva puta opciju A, jednom bi trebali dobiti, jednom izgubiti. Znači kući odlazimo s istom bankom s kojom smo i došli (Pod uvjetom da je prvo bio dobitak, zatim fulanac)
B?
Statistički ako bi odigrali 36 puta, jednom od toga mora biti nesretni 36-ti broj. Da vidimo, dobijemo 35 puta. 35 x 3000=105 000kn …zatim 36-ti put izgubimo banku i ostanemo bez naših 100 000kn. Trebali bi opet biti na nuli, ovih naizgled 5000kn viška su zato jer sam koeficijent 1.028 zaokružio na 1.03. (To će vam ujedno pokazati kakve pomake radi prisutnost zelenog polja(nule)) …samo ona okreće stvar u negativnom smjeru. Zbog nule je pravi koeficijent 1.02777 za ovaj slučaj… no nebitno sad to…
Ok, još se nismo dotakli bankrot sistema. …ovo gore je bio čisto pokazatelj kako koeficijent radi…i da ukoliko je koeficijent pošten i statistika točna (a na duže staze je) …da se zarada drži NULE, isto kao i gubitak.
E sada, što je caka kod bankrot sistema / tog progresivnog ulaganja.
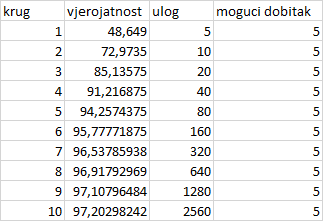
Recimo započnete s 5 kn na boju…fulate pa stavite 10, pa 20, pa 40 i tu dobijete 80kn.
Ukupni ulog je bio 5+10+20+40 = 75, a dobitak 80. Znači, dobitak je samo 5kn. (I biti će uvijek 5kn, bez obzira u kojoj fazi se desi pogodak. Tj…biti će uvijek onoliki s koliko ste započeli prvi krug.)
No koliki smo koeficijent zapravo igrali?
Dali je ulog 75 ,a dobitak 80? To bi bila kvota 80/75=1.0666 …ali neeee…mnogo krivi pogled…
Ulog je onoliki koliko smo riskirali novca…u slučaju bankrot sistema, ulog je onoliki s kolikom bankom igramo …jer u slučaju ako se ne dobije tih 5kn, ostat ćemo bez cijele banke. Znači riskiramo 100 000 kn radi 5kn. Oke…to je prilično sigurnih 5kn…naravno zato jer je kvota 100 005 / 100 000= 1.000005.
To je jako mali koeficijent…što znači i jako siguran. Ali to znači da riskiramo i veliki ulog za jako mali dobitak. A gornji primjer sa situacijama A i B nam je pokazao da nema boljeg i lošijeg koeficijenta ako su matematički jednako dobro posloženi. I upravo zbog ovoga ovaj sistem djeluje privlačan i siguran…jer se dobitak sakrio iza jako malog koeficijenta. No osoba ne vidi na prvu da s malim rizikom ide i mala dobit …jer mu se čini jednostavno ponavljati postupak koliko god puta treba da dođe do željene dobiti…a tu vreba nesreća. Ponavljanjem dobitaka se povećava dobit, ali i rizik …a omjer rizika i dobiti se nije niti malo pomakao od matematičke ravnopravnosti.
Jer kad se određeni koeficijent ponavlja više puta, onda više nismo igrali sigurni koeficijent od 1.000005.
Kada igramo više krugova određenog koeficijenta…onda je šansa da sve krugove dobijemo jednaka umnošku koeficijenata svih krugova. (Međuostalim, zato se množe kvote na listićima kladionica itd.)
Znači, da ćete dva puta pogoditi koeficijent 1.000005 šanse su vam 1.000005 x 1.000005 =1.0001
E sada, ajde da vidimo koliko bi netko htio zaraditi sa svojom bankom od 100 000kn. To je jako bitno pitanje…o tome ovisi kolike su šanse da to zaista i uspijete zaraditi. Npr. ako želite zaraditi samo 5kn …imate velike šanse za to. Ali ako želite zaraditi novih 100 000 kuna, onda je pitanje što vas čeka na tom putu…
…pa da vidimo…
Ajmo da osoba sa bankom 100 000 kn želi zaraditi 3000kn. Pošto će svaki ciklus maksimalno dobiti 5kn, mora odigrati ukupno 600 ciklusa da zaradi svojih 3000kn. Znači 600 puta se mora izložiti riziku 1.000005 da bi došao do zarade od 3000kn.
Da izračunamo koliki je to koeficijent, moramo 600 puta množiti 1.000005 sam sa sobom…tu će nam pomoći potenciranje: 1.000005^600 = 1.03 (Dali vam je taj koeficijent od nekuda poznat??) Vratimo se u primjer B s početka priče i vidjet ćete da je tamo također koeficijent 1.03 da osoba zaradi 3000kn sa bankom od 100 000kn.
Znači bankrot sistem nije niti malo povećao šansu dobitka …samo je prisilio korisnika da igra sa velikom bankom. Ono što je još gore…prisilio ga je ra proda kuću kad ostane bez banke bez koje ionako već nije smio ostati…nadajući se da će ga onaj sljedeći korak vratiti u život.
Znači, sasvim su jednake šanse doći sa 100 000kn i zatvoriti 35 brojeva od 36 …i dići 3000kn …kao i doći sa 100 000kn i odigrati 600 ciklusa bankrot sistema da se dođe do iste zarade.
Poanta je … omjer dobit/rizika se ne može povećati. Može se povećati šansa za dobitkom, samo ako se proporcionalno poveća i ulog koji se riskira.
A za one koji misle da bi jako velika banka ipak riješila stvar, postavit ću jedno “jednostavno” pitanje:
Koliko bi bio debel papir kada bi ga presavili 50 puta?
Zamislimo da je taj list papira u startu debel 1/10mm i teoretski da ga možemo savijati 50 puta bez da ostaje ikakav zrak među presavijenim slojevima…
…nadam se da bude netko izračuno, jer rješenje je više nego dobro.
Roulette je zlo!
Ako netko ne zna koji je zbroj brojeva rouletta neka ih zbroji i sve će mu biti jasno. Dakle 0+1+2+3+4+5+…+32+33+34+35+36=?
Slučajno? Ja vjerujem da ne.
Naigrao sam se tog sranja za 5 života. Izlazio sam iz casina sa desecima hiljada kuna nekad, ali sam i znao ulazit sa desecima hiljada i izlazit bez lipe. Najčešće sam igrao s par hiljada i puno češće sam gubio nego dobivao.
Elektronski i online roulette je programiran (namješten). Tu nema nikakvog spora. Točno se zna koliko će novaca svaki roulette ukupno isplatit. Elektronski offline zadržava puno više nego online roulette. Neki online roulette garantiraju 97% isplata što znači da zadržavaju 3% od svih uplata. Offline elektronski najčešće zadržavaju i do 40% uplata. Ne govorim napamet niti pretpostavljam.
Offline live roulette je samo malo pošteniji, ali i dalje nije fer. Uz to što roulette ima uvijek prednost baziranu na samoj igri (“0” i “00” u američkom ruletu), imaju i istrenirane krupijee. Pričao sam sa njih nekoliko koji su radili u luksuznim casinima vani i svi su mi rekli da im je jedan od glavnih uvjeta za dobiti posao bio da pogode određeno polje. Dakle ne broj jer je to nemoguće, ali određeni dio kotača da.
Onda još jedan vlastiti primjer. Igrao sam na bwin online roulette i ušao sa 50 EUR. Na isti stol je odmah iza mene došla neka ženska (mislim da je ženska jer je ona ikona pored njenog nicka bio ženski lik) koja je ušla sa 3000 EUR. Ja sam igrao na sitno i stalno padao i dizao se za 20-30 EUR. Tako je bilo sve dok je ona bila i dalje na oko 3000 EUR. Onda je počela masovno gubiti i ja sam počeo dobivati. Ona je pala na nekih parsto eura, a ja sam se digao na 2850 EUR (točno se sjećam iznosa). Pošto kad igraš roulette izgubiš svaku vezu sa zdravim razumom (znanstveno dokazano jer se aktiviraju svakakvi dijelovi mozga, stavljali su ljudima elektrode dok igraju i mjerili aktivnost mozga) ja nisam izašao i pokupio lovu nego sam igrao dalje. Počeo sam naravno gubiti, a istovremeno je ta ženska počela dobivati. Ja sam pao na nulu, a ona se opet digla na preko dvije hiljade eura. Tad sam popizdio i izašao pa ne znam kako je ona prošla do kraja.
Dakle čisti dokaz da ne možeš dobiti ono što netko već nije izgubio. To i ne bi bi bio problem da znaš unaprijed da će roulette isplatiti ono što je netko izgubio odmah nakon što taj netko izgubi. Nekada roulette danima uzima pa danima daje, a nekada uzme i odmah u slijedećoj ruci nekome da.
Uglavnom, klonite se toga jer je bolje trošit taj novac na drogu, alkohol i žene nego na roulette. Bar ćete imati zanimljiva iskustva. Ako baš morate kockati, kladionica je puno bolji izbor jer su puno veće šanse za dobitak (iako je i to sranje ako se pretjeruje).
A što se tiče ove stranice iz teme, to je čista prijevara. Vlasnik stranice skuplja proviziju od casina koju će mu isplatiti na svaki gubitak budale koja se registrira preko njega i krene igrati. Niti prva niti zadnja takva stranica. Čak postoje indicije da su tu “shemu” pokrenule same online kladionice.
Inače, prodao sam dosta domena iz niše “online gaming” i znam da je affiliate biznis u ovoj niši jako razgranat i jako profitabilan. Jedan čovjek s kojim sam trgovao danas imao doslovno milijune funti, a bio je običan službenik prije desetak godina. Onda je počeo sa promoviranjem online casino i kladionica i zaradio doslovno milijune. Samo što on ne vara posjetioce svojih webova nego radi realne recenzije casina i obaviještava o trenutnim bonusima.
Zadnja domenu koju sam prodao iz ove niše je domena sa 4 riječi u .co.uk ekstenziji i prodao sam je prije dva mjeseca za četveroznamenkasti dolarski iznos, a registrirao je par mjeseci ranije za cca $7. Sad je na njoj web stranica koja nudi informacije o casinima koja daju bonuse. Taj tko je kupio domenu od mene ima hrpu takvih stranica, a sigurno mi ne bi platio toliko za domenu da ne zarađuje dobro i da nema love. Znači ako je nekome do casina, neka se baci na affiliate u toj niši. Ako će raditi kvalitetno probit će se, a kad se probije bez problema će moći zaraditi i hiljadu funti dnevno.
Znači, da ćete dva puta pogoditi koeficijent 1.000005 šanse su vam 1.000005 x 1.000005 =1.0001
Super si se raspisa i bas san se uzivia dok san cita, jedino ode jedan mali podbacaj - ispada da ti se vjerovatnost povecava, sta je nemoguce.
Za dva puta za redom ide (1/1.000005)*(1/1.000005)
Za dva puta, bez da su za redom ide 1/1.000005+1/1.000005 (cini mi se hehe)
Da mi nisi dragi clan foruma, ne bi te ispravlja 
Takoder odlican post mitok-a
A za ove koji mogu nasist opcenito na ove jednostrane kobasice tipa kako sam se obogatio u mjesec dana ili bio sam siromasan, a sad zaradujem 3568$ tjedno - ■■■■ ga, takvi ce naletit di nalete da nalete. Svako je bia takav dok se nije opeka, a ovi sta ce probat radit cuda na ruletu ce se itekako opec. Jer, ka sta si i sam napisa, ti na kraju moras bit spreman ulozit npr 50000 za 100000 kn da bi zaradia 5 kn. Dovidenja mozak i zivci haha, ne znan ko bi to izdrza, a kamoli da ne sppminjemo da svaki rulet online ima svoje limite, a neki cak i zabrane ako vide dq na sitno peglas s tim idejama.
Tako da, po meni je svako dalje raspisivanje suvisno, osim alo nece neko pokrenit temu o gambling affiliate
Ajmo ukratko za one koji neznaju Znaci na rulet su brojevi od 0 do 36 ukupno 37 brojeva. Crnih je 18 i crvenih je 18 i 0 nema boju…
Sansa da pogodite boju je 18/37 sto je cca 48.649% znači da je casino u prednosti 2.7%
Po mom izracunu tablica izgleda ovako
iz tablice se da iscitati da sansa da cemo 10 puta za redom promasiti 2.8% te da riskiramo 5115 kuna kako bi dobili 5.
Na duge staze je casino uvjek u dobitku.
Ali glavna prednost igrača moze biti u tome sto sam bira ulog sam bira kada ce uloziti. Ta prednost se najviše mogla iskoristiti u blackjacku. Ali kako je tehnika napredovala sada casina prate svaki korak igrača takoder koriste po 8 dekova, sve kako bi onemogućili igracima da zarade…
Svaka cast ljudima na ovako dugim postovima, ovo je birtija i mislio sam da cemo se ovdje opet zezat, prepucavat i trolat, kak to ide, ali ne ovdje ste se raspisali svaka vam cast.
@bozoou Jesi ti matematicar?
Ako jesi moram reci da si u top matematicara Hrvatske. Ne zbog toga sto si sad rijesio ovu tu neku jednazdbu niti izracunao ovo sve skupa i objasnio lijepo kao da smo u skoli.
Nego jednostavno zato jer ti to sto si napisao i izracunao razumijes. Jer ja osobno poznajem nekolicinu matematicra koji ovo sto si ti sad izracunao znaju izracunati, ali nikako da razumiju sto su izracunali. Odnosno i dalje vise na tom kotacu. Ali to je prica za drugi topic.
Istina , krivo sam ovo gore napisao. Ali ne matematički …nego sam se krivo “opisno” izrazio.
Htio sam reći
koeficijent je 1.00005 x 1.00005 =1.0001
…jer šansa je recipročna vrijednost koeficijenta. Veća šansa za dobitak znači manji koeficijent …i obratno. Ako je kvota npr 2, šansa je 1/2 = 0.5 ili ti 50% ako se izrazi u postotku.
Tako da ova gore pogreška nije utjecala na konačne brojke…no ipak sam negdje pogrešio i u izračunu.
Da se digne 103 000kn sa ulogom 100 000, matematička kvota je 103 000/10 000 = 1.03
No nakon moga izračuna koeficijenta za to putem bankrot sistema , kvota je ispala: 1.00005^600=1.030453761 …ovo se može činiti kao mala greška, ali greška je. Jer da nema greške brojevi bi se poklapali u decimalu.
Ono bitnije, ako se na ovaj isti način ide računati koeficijent za poduplavanje banke putem bankrot sistema ispast će 2.7 kvota umjesto očekivanih 2.
Negdje je greška…jer prije sam to dobivao u decimalu, al priču sam objašnjavao iz malo drugog kuta.
No i iz tog drugog kuta je suština bila ista …za ostvariti neku dobit putem bankrot sistema su šanse iste kao da se sav ulog stavi na samo jednu kvotu koja će rezultirati istom dobiti.
Hehe, mrzi me jedan frend iz srednje…a zgoda je bila sljedeća. Ja sam volio puno markirati…i znao sam napucati 200 izostanaka po polugodištu. Dolazim jedan dan u školu, a on mi na odmoru pokaže što su zadnji sat radili iz matematike. Bilo je baš da su taj zadnji sat otvorili novo poglavlje…ja sam znači ravno 5 min proučio o tome što su učili.
Krenuo sat…pita profka jel možda netko zainteresiran da odgovara. Ja se javio, došao na ploču i pobrao peticu.xd. Meni to čak niti nije ostalo u nekom posebnom sjećanju koliko njemu, hehe.
Uglavnom, da…matematika mi je oduvijek išla od osnovne i najviše sam ju uvijek volio. Ipak sam kasnije otišao više fizikalnim putevima (faks FSB) nego matematičkim.
A što se tiče kladionice i koeficijenata…s time sam razbijao glavu cijelu srednju…pa je ostalo nešto u glavi, hehe.
Vidiš, u pravu si, sad mi tek dođe do glave, a igran kladionu cili život 
P.S. Kakvi glupi smajlići, ne mogu prikazat kako san se od srca nasmija 
Kad smo već kod fizike…pa da vidimo kako i ona ima veze sa kladionicom i klađenjem, hehe.
Zadatak je izračunati ukupni koeficijent koji će predstavljati dva pojedinačna koeficijenta koji su međusobno kontradiktorni.
Npr. na nogomet 1 i X, ili ako želimo pokriti opcije 1 i 2. Ocke…to kladionice nude sa svojim 1x , 12 , 2x koeficijentima, no što bi bilo da ne nude?
Recimo da ganjamo vlastiti 1x koeficijent. Ideja bi onda bila uplatiti dva listića. Na jedan odigrati kombinaciju 1 , na drugi X. U slučaju 1 ili X ishoda, jedan listić će nam biti dobitni.
Recimo da je kvota na 1 = 2.2, dok je kvota na X = 3.3. …a mi želimo uložiti 20kn i imati jedinstvenu dobit u oba slučaja. Ne želimo rasporediti ravnopravno ulog na način: 102.2 i 103.3 …pa da nam se dobit razlikuje ovisno o tome što prođe. Tada nismo stvorili rezultantni koeficijent koji predstavlja 1X.
Znači mi želimo za jedan ulog (20kn) imati neku jedinstvenu dobit (D). …tada znamo da smo imali i jedinstveni koeficijent koji je “dobit/ulog”.
Fizikalno se to ponaša identično kao pad napona u paralelnim granama strujnog kruga
Zato jer se ulog ponaša kao struja. Dio struje/uloga može otići u jednu granu…dio u drugu. Suma uloga na svakog grani/listiću mora biti jednaka ukupnom ulogu. (Suma struje u svakoj paralelnoj grani, mora biti jednaka količini struje prije račvanja)
Fizikalno, u jednoj točci strujnog kruga možeš imati samo jedan potencijal/napon. Znači prije račvanja smo imali neki napon…i nakon račvanja ćemo imati neki novi napon. Znači pad napona u paralelnim granama strujnog kruga mora biti jednak. A znamo da je pad napona I x R. Znači u grani gdje je otpor ® veći, otići će manje struje. Dok u grani gdje je otpor manji…otići će više struje…
Kod kladionice, mi smo si postavili uvjet da nakon svake paralelne grane / listića…želimo da je konačna suma love jednaka. A u svakoj grani konačnu sumu nam predstavlja izraz Ulog*K . Već smo rekli da se ulog ponaša kao struja, a sada vidimo da je u istoj relaciji sa koeficijentom (K), kao što je struja sa otporom ®.
Jer u granu gdje je veći koeficijent K, tamo treba staviti manje uloga…i u granu gdje je manji koeficijent K, treba staviti veći ulog da osiguramo jednak ishod nakon obje grane.
Znači, sve je isto kao sa strujom i otporima. Pa hajde onda da iskoristimo formulu koja je već izvedena za izračun struje.
Fizičari žele znati prije paralelnih grana koliki će ukupni pad napona biti nakon paralelnih grana. Mi želimo znati kolika će biti dobit nakon paralelno odigranih listića. Oni znači traže ukuni R, mi tražimo ukupni K.
Ukupni R za (dvije) paralelne grane , formula je: (R1*R2)/(R1+R2)
Ajmo isto napraviti i sa koeficijentima s početka priče:
(K1K2)/(K1+K2) = (3.32.2)/(3.3+2.2) => K_ukupni=1.32
Da vidimo sada kako bi trebali raspodjeliti uloge.
Ako je ukupni ulog 20kn, a ukupni koeficijent = 1.32 , znači da bi trebali na kraju imati love: 20*1.32 = 26.4kn.
1.listić (opcija X , kvota 3.3 , izlaz treba biti 26.4kn …znači ulaz treba biti 26.4/3.3 =8kn)
2.listić (opcija 1 , kvota 2.2 , izlaz treba biti 26.4kn …znači ulaz treba biti 26.4/2.2 =12kn)
Zaista 8kn + 12kn predstavlja naš ukupni ulog od 20kn…a bez obzira na ishod (1 ili X) idemo kući sa 26.4kn.
Točno ovako i kladionice sumiraju kontradiktorne koeficijente kada kreiraju novi koeficijent. Možete slobodno po gornjoj formuli provjeriti da 1X koeficijent kojeg nudi kladionica, uvijek odgovara ovakvom zbrajanju koeficijenta 1 i X.
No ovakvo zbrajanje koeficijenata ipak otvara mogućnost da si kreirate neke koeficijente koje kladionica nije ponudila… no da se ne zavaravamo, nema tu kruha…ovo je samo zanimljivo podudaranje ponašanja parametara u opkladi i parametara u strujnom krugu.
Ali svakako može dobro doći prilikom izračuna nekih koeficijenata i lakše procjenjivanje istih.