Moram priznati da imas smisla za development ovih igrica - imas zicu za to.Sjecam se da si davno i za Lino radio neke igrice 
Moras malo poraditit na “sigurnosti” tako da se kroz konzolu ne moze raditi svasta 
Btw nisam valjda ja jedini koji je pokusao/uspio rijesiti tj. vidjeti rijesenje puzzle na drugi nacin ?
Ae…onda si me “gratis” razveselio, hehe.
Sjećam se i ja da si ti fejkao rezultate kod neke od tih Lino igrica, hehe. A vidio sam da si pokušao i ovdje prije nego si i rekao (I bio sam poprilično uvjeren da si to ti, mada nisam mogao biti 100%)…
…uglavnom, vidio jedan “finished” state, samo stanje puzzli nije nalikovalo na finish state, hehe.
A i prije samog finisha su se nešto čudno kretale, pa nakon što sam provjerio da repriza ne baca neke čudne bugove, sam zaključio da si drmao po nekim funkcijama kroz consolu. Ali dao si mi malo posla da provjerim jel repriza radi po očekivanom, hehe.
Uglavnom, ovo što si ti otvorio moju “sakrivenu” konsolu, i nije neki problem sigurnosti. (Ok, treba takve stvari zatvorit svima, to se lako može)
Ali ono što se ne može. Ne može se blokirati igrača da pošalje željene vrijednosti na server i da simulira da ih je poslala igrica. Na to su ranjive sve igrice…i općenito sve web aplikacije.
Kod dosta igrica je to velik problem, i to kod onih kod kojih nemaš način provjeriti jel rezultat nastao kroz igranje…ili je nastao slobodnim odabirom onoga koji prčka po consoli. (Naravno, može mu se to otežati…ali blokrati ga je nemoguće.) I zato nažalost pola online igrica nema realne rezultate u listi TOP igrača.
No kada imaš način provjere, onda mu je džabe što on ručno simulira rezultat.
Npr. kod ove igrice nije dovoljno poslati konačni state "finished=true" (koji si ti poslao trigiranjem funkcije onFinish()), kada uz taj state trebaju stići i koordinate puzzli koje odgovaraju složenom stanju. A “lopov” ako zna fejkati koordinate, onda zna i složiti puzzle.
To je uglavnom fina pogodnost ovakvom tipu igrice, jer nakon što složim spomenutu igricu sa levelima, moći će imati vjerodostojnu listu top igrača.
Dok recimo nekakvu igricu tipa “gađanje pikada” je teško zaštiti. Jednom dok “lopov” vidi koji su parametri uspješnog pogotka…umjetno nakrca svoj konačni rezultat sve sa uspješnim pogotcima…i ne možeš mu praktički ništa.
Možete se samo naganjati ko mačka i miš, da mu otežaš fejkanje i on da skužio caku koju si podvalio i da je probije…pa tko je uporniji…
Hehe, ugly5 ekipa captured.
Možda ni ovo nije ok, zbog spojlanja zagonetke…ali nije ni problem. I sam dvojim da ću za promociju ovih puzzli možda upravo reklamirati taj state i postaviti upitnikom:
“How to fit the remaining ugly5 pieces?”
Tako da gornji state nije problematičan što se vidi…al iskreno se nadam da neće biti onih koji će spojlati i konačno rješenje. To ću staviti u pravilnik da je ilegalno prema TOS-u puzzli 
Fala. Ovo su ti inače poprilično zabavne vode.
Ovdje ti ne treba preveć kompleksnog programiranja, do izražaja više dolazi poznavanje matematike i nešto fizike. Ali ništa prestrašno.
Sada si me naveo baš da prokopam malo po bilješkama tih igrica, da se prisjetim čega je sve tamo bilo zanimljivoga xd.
Krenuvši od ovih puzzli, a i u većini igrica su matrice rotacije i translacije neizbježne:
Moram priznati vrlo nezgodne su bile u ovim puzzlama gdje postoji koordinatni sustav flipan oko horizontalne osi i koordinatni sustav flipan oko vertikalne osi.
Ako ništa drugo,naučio sam u ovome da koordinatni sustav koji je flipan i oko vertikalne osi i oko horizontalne osi, je isti originalnom koordinatnom sustavu zarotiranom sa 180 stupnjeva. Nekako zanimljiv mi fact.
Onda dok se prisjetim računanja odbijanja u sva četiri kvadranta:
Pa računanje koji objekti su u perspektivi kamere:
Nekad su skice poprilično šarene xd:
Pa računanje kolizije između objekata:
Inače, što se tiče kolizije objekata…to i nebi bio toliki problem izračunati da nemaš diskretnu vremensku os u igrici. Diskretna znači da imaš pauze između momenta t1 i t2 u kojem računaš stanja objekata. Moraš imati pauze, jer namaš beskonačnu procesorsku snagu koja bi to mogla računati kontinuirano za svaki moment t…kao što to svemir nekim čudom odrađuje za našu fiziku u beskonačno t momenata.
Pa tako recimo ako imaš loptu koja pada prema podu, ti ćeš njezinu poziciju izračunati u prvoj milisekundi, pa u 10milisekundi, pa u dvadesetoj…itd. Ovisi koliki interval već zadaš…
Pošto znaš početnu brzinu i poziciju lopte, te znaš i kolka je gravitacija koja djeluje na nju…onda u svakom tom momentu t možeš relativno lako izračunati njenu novu brzinu i put koji je prešla između prošlog t i trenutnog t. I tako u svakom tom intervalu računanja pronalaziš nove koordinate x,y,z lopte, te kooridnate transformiraš u 2D sustav kako bi dobio ekvivalente x,y koordinate i renderiraš loptu na toj x,y pozicji. I to je sva mudrolija za tijela koja se gibaju i na koja utječu neke sile…nije iza toga uopće neka strašna fizika.
I onda dalje kada vidiš da je lopta po visini došla ispod razine podloge, shvaćaš da dolazi do odbijanja…mijenjaš smjer brzine lopte, tako da paziš da ti je upadni kut vektora brzine isti izlaznom kutu. Također, da bi se realno odbila, dodaješ i nekakav koeficijent odbijanja…tako da iznos brzine nakon odbijanja bude umanjen prema tom koeficijentu od ulazne brzine prije odbijanja.
I tarannn…lopta se odbila od podloge i dalje ide u zrak. Zbog utjecaja gravitacije na vektor brzine, stat će u određenoj točki i opet se krenuti gibati prema dolje.
Ako koeficijent odbijanja postaviš da je 1, onda ćeš imati savršeno odbijanje…ili ti ga lopta će odskakati od poda beskonačno puta.
Probaj to složiti, baš je gušt zavrtiti tako nešto. Ne moraš s loptom…možeš napraviti npr. da naslov web stranice padne i odbije se od dna stranice i da se vrati gore…hehe. Moglo bi se svašta igrati.
Ali ima nešto strašno…čega sam se usrao kada sam shvatio koliko podiže kompleksnost za neke malo kompleksnije koolizije tijela.
Pošto imaš diskretne momente kada računaš poziciju lopte, to znači da ti nećeš računati koliziju točno u momentu kada je ona takla podlogu…nego ćeš računati njenu poziciju barem neki mali trenutak nakon što je ona trebala već taknut podlogu. A to znači da su vanjske koordinate lopte malo zašle u podlogu prije nego joj ti okreneš smjer kretanja.
U nekim jednostavnim stvarima to uopće ne stvara problem…ali stvari neće biti idealne. Recimo, gore sam spomenuo da koeficijent odbijanja ako je 1, da će se lopta odbijati neograničeno puta…svaki puta isto.
E pa zbog te male greškice ipak neće biti tako. I lopta će se svaki puta manje i manje odbiti…bez obzira što je koeficijent=1.
Izuo me iz gaća taj “bug” dok sam prvi puta shvatio što se dešava. Tu grešku za loptu i nije bilo tako teško koregirati, mada nije bilo ni jednostavno. (Sljedeća slika je izračun samo za tu grešku kako je koregirati)
No kada imaš više tijela koja mogu doći istovremeno u koliziju, stvar postaje noćna mora. Istraživao sam kako veliki igrači to rješavaju i kada sam vidio metode…zasrao sam se. Toliko "diferencijalne "matematike u životu nisam vidio. 
To se zove i problem “leta metka” …jer ako želiš u tom svom t momentu kada računaš poziciju svakog tijela vidjeti da li je metak nešto pogodio…on ako je i pogodio svoju metu, vrlo vjerovatno je zbog velike brzine leta već daleko iza mete dok ti radiš kalkulaciju pozicija.
Pa ti onda više nije dovoljna pozicija metka, nego moraš računati i putanju metka da shvatiš jel bila koja meta na njegovoj putanji…što bi značilo da je pogođena.
Jednostavne stvari opet nisu problem, no što kada imaš metak koji se odbija od zidova i drugih tijela…koja se također međusobno odbijaju. E onda je fakat kompleksan problem.
Ili tri kugle koje se istovremeno sudaraju…pa ti računaj koja kugla je koju prva lupila i koji su izlazni vektori brzina.
A što tek kada imamo kugla u kontaktu kao u sljedećem videu:
)
Da se svašta izguglati o tom problemu i slike na sljedećem linku će bolje dočarati što sam rekao:
@bozoou, nisam u tome, pa nisam znao koliko treba truda i koraka napisati do takve igrice svaka ti cast !
svaka čast bgmi si prekucao igricu
Fala, al trebalo je dočarati koliko je jednostavno Ok, izvukao sam neke higlighte problematike, pa zvuči malo teže.
Evo zato u nastavku minimalno što je potrebno da se napravi 2D model gibanja nekog tijela. Što je osnova više manje za svaku igricu:
(Nakucao sam iz glave…možda ima neka bezvezna greška. Ali to je code koji bi praktički mogao raditi)
var lopta = {
x:0,
y:10, //znaci lopta se nalazi na 10 visine. 10 čega? Pa metara ako je i sve ostalo u standarnim mjernim jedinicama
vx:0, //brzina po x osi neka je nula. (Horizontalna brzina je znači nula)
vy: //brzina po y-osi neka je nula (Vertikalna brzina je znači nula)
ax: 0, //akceleracija po x osi neka je nula. (Horizontalna akceleracija je nula, ako nemamo tijelo koje gura loptu po horizontalnoj osi)
ay: -9.81, //akceleracija po y osi u negativnom smjeru je 9.81. Ako želimo bestežinsko tijelo onda je nula. Ako želimo invertirati gravitaciju da tijelo pada prema gore...samo okrenemo predznak. U našem svemiru, mi smo Bog koji bira pravila :D.
}
/*
Kada bi bio 3D prostor, onda bi još trebali dodati lopti
lopta.z;
lopta.vz;
lotpta.az;
Računanje pozicija i vektora brzine tada i nije ništa kompleksnije. Problem je grafika koju treba renderirati kod objekata koji su zamišljeni da se nalaze u 3D prostoru
A sada kako je jednostavna fizika računanja vektora brzina i pozicije.
Prvo treba startati timer koji će u određenim invervalima delta_t računati pozicije:
*/
var delta_t=1000/23; //23 frame-a per second je čisto dobar izbor. Ne prezahtjevno procesorski, a oko ionako ne vidi više sličica u sekundi pa nema potrebe za većom rezolucijom kalkulacije.
var t = delta_t/1000; //čisto da imamo delta_t izražen u sekundama, koja je standarna mjerna jedinica za vrijeme.
var mainloop = setInterval(function(){
//prvo izračunati novi vektor brzine koji imamo nakon perioda delta_t. Ako smo imali akceleraciju koja je djelovala na loptu, očito se promjenila i brzina lopte. Izračunajmo novu brzinu:
lopta.vx = lopta.vx + lopta.ax*t;
lopta.vy = lopta.vy + lopta.ay*t;
// vidimo da je lopta dobila neku brzinu u ovih delta_t, što znači da joj se mijenjala i pozicija.
// Treba izračunati i nove koordinate pozicije:
lopta.x = lopta.x + lopta.vx*t;
lopta.y = lopta.y + lopta.vy*t;
//taran...imamo svježe x,y koordinate lopte za ovaj moment t..sada treba samo pozvati još funkciju koja će renderirati objekt loptu, a to je ništa drugo nego da je postavi na odgovarajuću poziciji prema njenim koordinatama.
//i ako činimo to konstantno za svaki moment t, oko će zbog konstatnih promjena koordinata vidjeti i brzinu lopte i akceleraciju lopte.
renderObjekt(lopta);
//Čiča miča, gotova priča.
},delta_t);
I to je to. U praski nije jedino tijelo lopta koje imamo, pa treba napraviti loop i odraditi kalkulaciju pozicija za svako tijelo koje se nalazi u igrici.
A dalje je sve logika koju ćemo na to nabacati. Recimo ako tijelo nije lopta nego nekakav platformer junak. Onda se povežu inputi sa tipkovnice:
var brzinaJunaka=5;
var snagaSkokaJunaka=6;
KeyLeft.onclick = function(){
junak.vx = -1*brzinaJunaka;
}
KeyRight.onclick = function(){
junak.vx = brzinaJunaka;
}
//još bi trebalo pripaziti kada nijedna nije pritisnuta da je vx=0;
KeyUp.onclick = function(){
//provjerimo da li se junak nalazi na podlozi i samo ako se nalazi onda može skočiti:
if(junak.y==0)junak.vy = snagaSkokaJunaka; //i junak će skočiti. A za to da padne opet na tlo će se pobrinuti akceleracija koja mu mora biti dodjeljena isto kao lopti. Inače će odletiti u svemir :D :D
}
Znači, ništa prekompleksno.
Ali naravno kao i svugdje, uvijek bude problemčića koji se putem sretnu. Sve ovisi koliko kompleksne stvari želimo praviti. 
P.S.
Ovakav junak nebi baš smooth ubrzavao smjesta, pa bi bilo još bolje njegovo kretanje upravljati preko njegove akceleracije, tj. ax komponente akceleracije.
Ali, ako imamo akceleraciju koja djeluje na tijelo…brzina tog tijela bi rasla s vremenom u beskonačnost.
U realnosti ne raste…jer se sa brzinom pojavljuju otpori koji neutraliziraju silu koja gura i stvara akceleraciju. U platformeru bi to vrlo jednostavno ograničili…samo bi rekli ako je brzina kretanja veća od neke max definirane, da više ne raste.
Ili ti ga u onom mainloopu bi stajalo:
if(platformer.vx > platformer.max_v) platformer.vx = platformer.max_v;
else if(platformer.vx < -platformer.max_v) platformer.vx = -platformer.max_v;
//ili da isto zapišemo na lijepši kraći način:
if(Math.abs(platformer.vx) > platformer.max_v) platformer.vx = platformer.max_v * predznak(platformer.vx); //predznak je očito funkcija koja vraća predznak (-/+) nekog broja
…i tako, igrarija uglavnom.
Ups, zalomila mi se jedna greška iz fizike. Trenutno sam na mobu, pa ispravim kasnije. Fizika je srednjoškolska pa je može ispravit i netko drugi.
Svi su laki na okidaču kad treba zaključit da sam lud, valjda netko od tih zna i fiziku srednje škole.
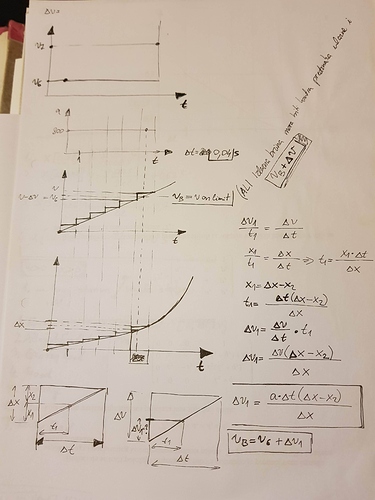
Kad sam već započeo, da ispravim i grešku. Jer stvarno, temelj engina za 2D paltformer igricu je ono gore. Stvarno nije nauka i svatko bi se mogao okušati napraviti igricu
No zalomila mi se greškica u računanju koordinata i ispravak je sljedeći:
lopta.x = lopta.x + lopta.vx*t/2;
lopta.y = lopta.y + lopta.vy*t/2;
E sad, ako bi zavirli u knjige fizike, vidjeli bi da je to formula za izračun puta koje prelazi tijelo koje ubrzava konstantnom akceleracijom.
No u istoj toj knjizi ima hrpetina formula …te za ovakvo ubrzanje, te za onakvo ubrzanje…te za gibanje konstantnom brzinom…pa za kosi hitac…pa slobodni pad…pa vertikalni hitac…itd…itd. Čovjeka od svih tih formula može samo zaboliti glava.
A postoji suvše lak način da sve te formule imate zauvijek u glavi ako zapamtite samo dva pravila.
Pošto je izračun brzine tijela i pozicije tijela… temelj svake igrice, ovo je svakako jako korisno razumjeti…pa ću biti dobre volje objasniti ta dva pravila.
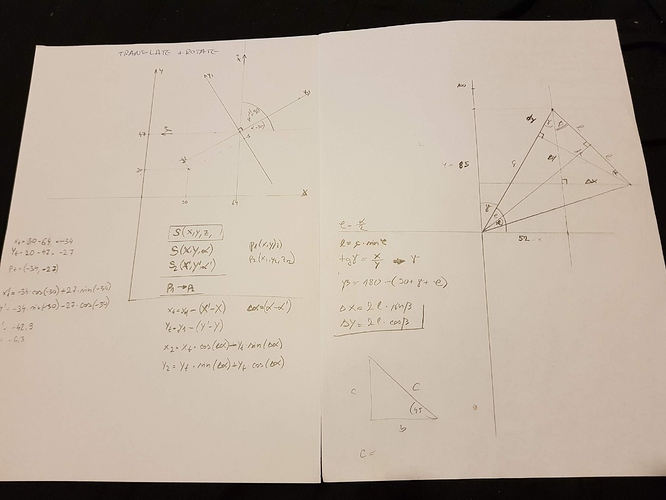
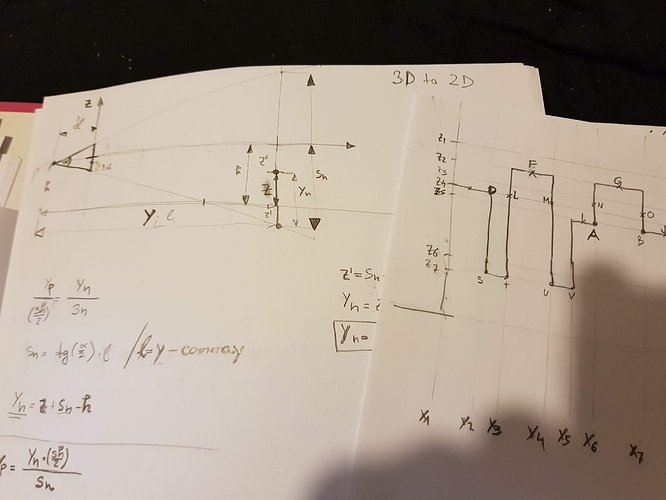
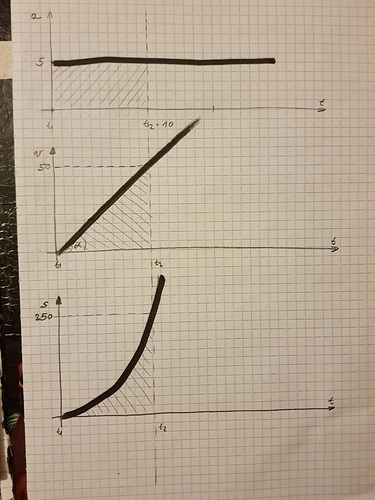
Za početak slikica koju ću komentirati:
Na skici se vide tri grafa.
Primjetimo da je x-os zajednička za sva tri grafa i ona predstavlja vremensku os. Na toj vremenskoj osi sam označio dva momenta. t1 i t2. t1=0 i t2=10. Što znači da promatramo što se dešava sa tijelom od nulte sekunde do 10 sekunde njegovog gibanja.
Valja spomenuti da na tijelo u momentu t1 počinje djelovati nekakva sila, koja rezultira njegovim ubrzanjem. To vidimo u prvom grafu da nam je akceleracija konstanta i u svakom momentu iznosi 5.
Kako tijelo ubrzava, očito mu sa svakim sljedećim trenutkom raste brzina. To vidimo u drugom grafu kako brzina konstatno raste. Tijelo je znači mirovalo u trenutku t1 jer je tada brzina bila 0. Nakon toga pod utjecajem sile tijelo ubrzava, tj. brzina mu konstatno raste.
Treći graf prikazuje prijeđeni put. Normalno da tijelo koje ima neku brzinu, prelazi i put. No kako je brzina u svakom momentu sve veća i veća…očito će u svakoj sljedećoj sekundi tijelo uspjeti prevaliti veći put nego u prethodnoj sekundi. Zato nam graf prijeđenog puta izgleda tako “eksponencijalno”.
I sada ono bitno. Treba shvatiti koje su relacije između ta tri grafa. To je podosta dobro razumjeti, jer te iste relacije postoje svuda u svemiru. One nisu nešto što se tiče samo sprege “akceleracija, brzina, put”.
Valja primjetiti i da te tri stvari promatranja: “akceleracija, brzina, put”, su praktički samo jedna stvar.
Ako se sjetite mainloop gore iz programskog coda, vidjet ćete da ja nigdje nisam renderirao brzinu ili akceleraciju u slici. Ja sam samo renderirao loptu na njenoj x,y poziciji za svaki moment t. Brzina i akceleracija se pojavljuju kao posljedica renderiranja lopte na različitim pozicijama. Znači postoji samo lopta na nekoj poziciji u nekom momentu t. Promjenu te pozcije lopte mi opažamo kao brzinu lopte…pa i kao akcelerciju lopte.
Zašto bi tu stali? Pa postoji tako i akceleracija akceleracije. Pa akceleracija akceleracije akceleracije…itd u beskonačnost. Znači suštinski postoji samo pozicija lopte, a sve drugo su “efeketi” koje opažamo zato jer lopta mijenja tu svoju poziciju.
To se matematički kaže:
Nemojte da vas uplaši riječ derivirati. Vrlo je jednostavno, derivacija je promjena iznosa nečega
Tako je brzina promjena pozicije u vremenu
A akceleracija je promjena brzine u vremenu
I zato sam gore rekao da ono što ću objasniti je primjenjivo na svašta, jer sve stvari u svemiru prolaze svoju promjenu …ne radi se tu samo o promjeni pozicije, što vidimo kao brzinu. Isto se čak preslikava i na psihološke stvari, jer i sreća je čak promjena nečega…sreća je derivacija nečega. I kad se shvati čega, lakše je nekako razlučivati bitno i nebitno… …vratimo se na fiziku
Sada kada sam objasnio što je derivacija, valja spomenuti što je obratni proces. Obratni proces se zove integracija.
Pa je tako brzina integral akceleracije po vremenu
A prijeđeni put je integral brzine po vremenu.
I evo nas kod derivacija i integrala…odlična dva alatića koja su nehotice ozlogašena i neshvaćena od šire publike. A nisu uopće strašni kada se shvate. Ne kada se nabubaju njihove formule, nego kada se vizualno shvati što oni predstavljaju.
Prije nego se vratimo na grafove, ukratko što je integral i derivacija u vizualnom/geometrijskom smislu.
Pa integral je površina ispod grafa, a derivacija je kut tangete grafa.
Huh, zbunjujuće zvuči…ali dječja igra je. Pazi dalje…vratimo se sada gore na graf akceleracije.
Kolika je površina ispod grafa akceleracije između momenta t1 i t2?
Vidimo da je to pravokutnik kojeg zatvaraju stranice dužina 5 i 10, te je onda površina = 50.
Kako je brzina integral akceleracije, to znači da brzina u momentu t2 mora biti 50.
Ajmo to logički opstruirati. Ako tijelo ubrazava iznosa 5.
(Čega 5? Pa 5 brzina po sekudni. A pošto je jedinica brzine “m/s” …onda imamo (m/s)/s i dobivamo da se akceleracija izražava kao “m/s^2”)
Znači ako ubrzava 5 brzina po sekundi, znači svake sekunde će brzina narasti za 5. I nakon 10 sekundi će logično brzina biti 50. I to je po geometriji ta površina ispod grafa.
Ajmo izvesti formulu za isto, kolika je površina ispod grafa? Jedna stranica nam je “a” druga je (t2 - t1) ili ti ga delta_t (dt). Znači površina ispod grafa je “a * dt” …iz čega dobivamo formuli za promjenu brzine:
“dv = a * dt”
Zašto je to formula za promjena brzine (dv)? Zašto to nebi bila formula za konačnu brzinu u momentu t2?
Pa zato jer integral između momenta t1 i t2 nezna ništa o stanju brzine koja je bila prije momenta t1. Moglo je tijelo do momenta t1 već juriti 100m/s, što znači da bi se između t1 i t2 tijelo opet ubrzalo za 50m/s, ali bi mu konačna brzina onda bila 150m/s.
Što će nam reći, da kod integriranja uvijek moramo znati koliko smo imali početno stanje i pribrojiti ga rezultatu integriranja. Prema tome imamo kompletnu formulu za brzinu:
v2 = v1 + (a * dt)
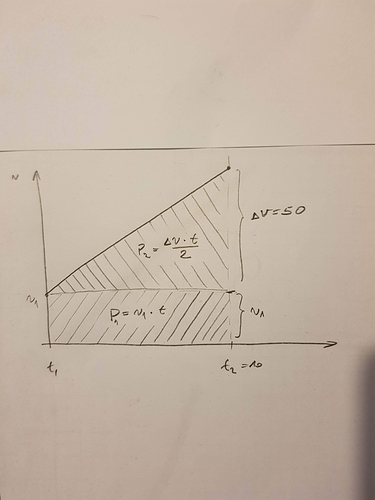
Ajmo sada izvesti formulu za prijeđeni put. Znači isto površina ispod grafa, ali ovog puta površina grafa brzine. Vrlo jednostavno:
s2 = s1 + (v2*dt/2);
s1 je početno stanje prijeđenog puta i isto ga moramo uračunati kao i početno stanje brzine.
v2*dt/2 je ništa drugo nego površina ispod grafa brzine…gdje ovog puta imamo trokut, a poršina trokuta je ekvivalent polovici povrišne pravokutnika. I zato moramo podijeliti sa tih dva.
Morate uvidjeti da smo vrlo vrlo jednostavno došli do formule koja i nije tako banalna:
s2 = s1 + (v2*dt/2);
I to je to prvo predivno pravilo. Integral je površina ispod grafa.
Raditi bilo kakvu fiziku, pa i onu najosnovniju…bez toga je jednostavno glupo. Mogu reći da je sramota za srednju školu da preskaču tu lekciju o integralima. Fizika postaje daleko jednostavnija kada se to shvati.
Drugo pravilo drugi puta…bilo voljnih poslušati ili ne. xd
Evo malo drugačijeg setupa iste zagonetke.
Nekako mi se čini da je zanimljivija ako se zada na sljedeći način: http://www.technoangels.hr/index.php?page_path=ugly4?only4=true
…da se kreće odmah od zagonetnih puzzli?
Btw. više nije ugly5 nego ugly4
Hmm sta je tacno drugacije meni je isti fazon osim sto je na pocetku namjerno slozena pogresno?
Zacudo trebalo mi je 22 minute, a mislio sam da cu je sloziti za 5 minuta. Lagano je otici u krivom pravcu, ili da ne vidis neki flip and rotate.
Kada bih htio kupiti ovakav puzzle, a da nije virtuelni, sta bih trebao da guglam, jel ima neki naziv?
Pa to je drugačije. Koliko vidim po statistici, oni koji se uhvate problema se bome bave sa puzzlama podosta vremena.
No za većinu to izgledaju kao sasvim obične puzzle i napuste stranicu unutar jedne minute.
Nije da mi je ovo komercijalni projekt pa da želim zbog toga produljiti da ostaju…ali svejedno želim na najbolji način dati te puzzle drugima, a to se očituje kroz vrijeme slaganja.
Ako ih puzzle dočekaju u stanju da trebaju rješiti samo ugly4 ekipu, onda su možda intrigantnije i zanimljivije potencijalnom igraču.
No s druge strane, gubi se ona draž da ih igrač složi i taman misli kako je gotov…a ono čorak.
Pa mi je malo teško odvagnuti između toga dvoje. Vidjet ću malo ovako kako će se ponašati statistika pa odlučiti…
Keywordi bi možda mogli biti “logic puzzle”, “IQ puzzle” …ali tu opet upada svašta. Jer imaš puno logičkih slagalica koje nisu ovako klasične 2D puzzle …a spadaju pod te keyworde.
Ja inače imam hrpetinu tih logičkih slagalica doma…praktički naručujem svaku novu koju opazim da postoji, hehe …pa moram priznati da ih nisam našao puno u ovom obliku 2D puzzli.
I onda sam slučajno naletio na jedan izvor i sada znam za 4 baš odlične. Sve 4 će uskoro biti na ovoj mojoj stranici, a imat ću ih i u prodaji.
A gdje si kupio ili kako si napravio ovu? Ovo mi izgleda ekstra.
Ja bih ostavio prvu varijantu kad naletis na onih 5 zadnjih, jer tu te bas natjera da razmisljas nanovo i gdje si upao u logicku gresku.
Napravio sam ih i da…ekstra su.
Gore kažem da ništa nije sakriveno, ali tehnika izrade će ostati ipak mala tajna.
Slažem se, vjerovatno ću i ostavit na kraju tako.
https://www.puzzlemaster.ca/browse/novelty/packing/12395-jigsaw-puzzle-29
Ova izgleda jako slicna toj tvojoj. Akril cak i i vidim da se figurice poklapaju? Jel ovo ti prodajes?
…nastavak avanture korisnoga znanja.
Za početak, gore mi je opet promakla jedna greškica. Ali to je dobro kod grafova i razumjevanja istih…možemo bez kopanja po formulama utvrditi da smo napravili grešku, te sami se koregirati i doći do ispravne formule
Puno vrijednije nego slijepo korištenje formula i ne mogućnosti uopće da uvidimo ako griješimo.
Uglavnom, gore sam pretpostavio da imam početnu v1 brzinu, iako je ona prema početnom stanju jednaka nuli. Ali ako želimo imati formulu koja opisuje jednako dobro gibanje i koje ima početnu brzinu i koje nema početnu brzinu…onda je bitno pretpostaviti da postoji taj v1 i uključiti ga u izračun.
Tako da konačna gore formula za prijeđeni put nije potpuno točna…tj. točna je samo za ona gibanja koja se kreću gibati sa mjesta.
Pa da proširim to, dodao sam u drugi graf brzina da postoji početna v1 brzina. Slijedi slika grafa:
Vidimo sada da ta početna v1 brzina stvara dodatnu površinu ispod grafa koja je:
P1 = v1 * t
a P2 je površina koju smo imali i ranije: P2 = dv*t/2
Kako smo rekli da je prijeđeni put integral brzine, znači površina ispod grafa brzine, tako formula za prijeđeni put slijedi:
s2 = s1 + v1*t + dv*t/2;
Heto, naš prvi izračun bi bio točan…jer nam je v1 bio nula, pa je površina tog pravokutnika bila nula, tako da nam taj član ništa nebi promjeio u gore konkretnoj situaciji…ali nismo ipak imali “univerzalnu” formulu.
Kada već spominjem univerzalnu formulu, onda je dobro primjetiti koliki nam je dv. To smo imali ranije:
dv = a*t //Povrišina ispod grafa ubrzanja
…pa kada to uvrstimo u formulu za prijeđeni put, dobivamo:
s2 = s1 + v1*t + a*t^2/2;
Sada je to već formula koja može poprilično toga opisati…ali opet, razumjevanjem grafova se mogu opisati vrlo jednostavno ama baš sve situacije i vrlo lako intuitivno shvatiti što se dešava.
A formule se koriste kada ste na “ti” sa gradivom, pa ste sigurni koju uzimate i na taj način ubrzavate proces rješavanja.
Puno lakše je gradivo “vječno” upamtiti ako se upamte samo spomenuta dva pravila koja opisuju relacije između grafova …doduše, drugo pravilo još nisam opisao…pa evo slijedi…
Tu ne prodajem ja… i to ti je ova ista puzzla sa slike gore.
To je ujedno i puzzla koja me inspirirala da napravim ugly4 puzzle.
Te puzzle znači imaju 5 korner puzzli i ne idu sve rubne puzzle uz rub. Što je već poprilično cool i to mi se jako dopalo.
No ono što sam vidio kao manu tim puzzlama:
Stoga moj dodatak tim puzzlama je bio upravo da “izbacim” jedan korner i da omogućim da je okvir složiv iako je prava solucija sasvim druga. A to je bio hebački zadatak
